FROM ツバキ

 

先日、数学を指導していたところ、通分でつまづいている生徒さんがいたので、
通分に戻って学習をすることにしました。

そこで、通分のやり方を見ていると、

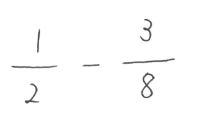
1/2の分子と分母をそれぞれ8倍、3/8の分子と分母をそれぞれ2倍してやっていました。

8/16-6/16=2/16で約分して1/8
となりますね。

どうしてそのやり方をしたの?と聞くと、
「下(分母)の数を反対にかければいいって先生が言っていた」と言うことでした。

1/2にはそれぞれ8を、3/8にはそれぞれ2を。

たしかに、それでもできます。

でも、約分するひと手間がいりますね。
そして、

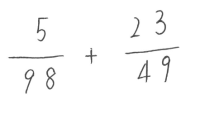
のように、分母の数が大きくなったらどうするのでしょう?

単純に反対にかけて･･･とすると、

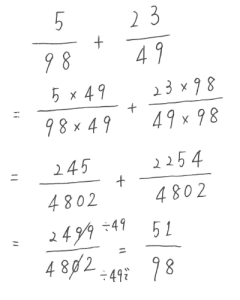
とんでもなく大きな数字になります･･･。

計算しづらいですし、ミスしやすくなりますよね。
それに、テストでは余計な時間をとってしまいます。

 

「通分」とは･･･?

説明では、
「分数を同じ分母にそろえることです。ふつうはそれぞれの分母の最小公倍数を選びます」とあります。

イメージしてみてください。

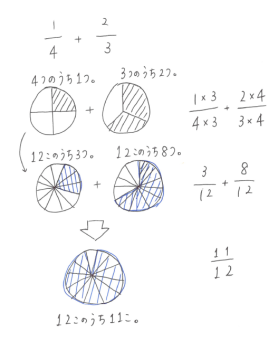
1つのパイがあって(ケーキでもいいですよ)、4等分にしてあるものと、3等分にしてあるものと、切り方が違うパイがあります。

「4等分の1つ」と「3等分の2つ」を合わせると、どれくらいの大きさになるでしょう?

･･･

切り方が違うので、単純に数字だけでは合わせられないですよね。

だから、切り方を一緒にして考えてみよう、というもの。

4と3に共通する倍数(最小公倍数)で一番小さいのは12ですね。
それで、両方とも12等分にして、大きさを合わせます。

だから、1/4と3/12、2/3と8/12は数は違えど、パイ自体の大きさは一緒です。

 

こうして考えると、
さっきの巨大な数字になったものの、

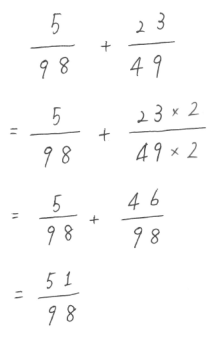
最初から最小公倍数98で考えると、ラクにできます。

 

なんでも、表面的なやり方、ではなく、
本質・考え方を大事にしたいですね。

ツバキ
(家庭教師のオアシス チューター/教務スタッフ)